In this problem, we have an exponential function of the form
y=a(b)^x
where
y is the population of San Diego
x number of years since 2012
so
Part a
2012 represents x=0, y=1,309,000
a=1,309,000
For the year 2016 ------> x=2016-2012=4 years
y=1,375,000
therefore
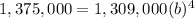
solve for b
b=1.0124
b=1+r
substitute and solve for r
r=1.0124-1
r=0.0124
percentage
r=1.24%
Part b
2016-2020
in this part
a=1,375,000
x is the number of years since 2016
For the year 2020 -----> x=2020-2016=4 years
y=1,386,000
substitute
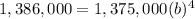
solve for b
b=1.0020
b=1+r
r=1.0020-1
r=0.0020
percentage
r=0.20%
Part c
Compare the growth rate each period
2012-2016 ------> r=1.24%
2016-2020 -----> r=0.20%
that means ----> in the second period the growth rate has decreased than the first period
Part d
the current growth rate is r=0.20%
so
the equation is
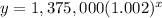
where
x is the number of years since 2016
so
For y=1,500,000
substitute

solve for x
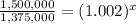
apply log on both sides
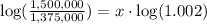
x=43.5 years
therefore
the year is
2016+43.5=2059.5 -------> approximate the year 2060