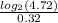Answer: B
Step-by-step explanation:
Step 1. The expression that we have is:
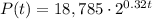
This represents the population P after t years.
Step 2. We need to find the expression that represents the amount of time, t, in years, for the population to be 88,740:
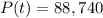
Step 3. Substituting this value of P(t) into the given equation:
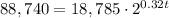
Step 4. To solve for t, first, we divide both sides by 18,785:
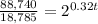
The result of the division is:
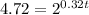
Step 5. Then, to continue solving for x, we apply the logarithm base two to both sides:
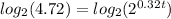
We simplify applying this property of logarithms:
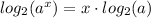
The result is:
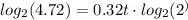
And since:
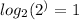
The expression now is:
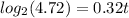
Step 6. Dividing both sides by 0.32 to solve for t:
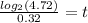
This expression is shown in option B:
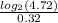
Answer: B