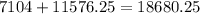Recall that the Doyle log rule formula is
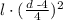
where l is the length of the log (in ft) and d is the log's small-end diameter (in in).
Recall that the total amount of usable lumber is the sum of the usable lumber of each log. So, we will calculate the usable lumber of one type of log and then multiply it by the number of logs of that type. Finally, we calculate the sum of all types, to find the usable lumber.
First we have the type of 10 feet long logs with 25 in diameter. For this type, we have l=10 and d=25. So we get
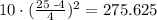
Of this type, we have 42 logs. So the total amount of usable lumber is
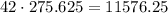
Now, for the other type of logs, we have l=12 and d=20. So we get
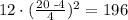
Since we have 37 logs of this type, the total amout would be
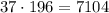
Then, the total amount of usable lumber would be