Question

Greg nada 100 yardas en 52 segundos. Kelly planea nadar 150 yardas al mismo ritmo. ¿Cuántos segundos le tomará completar su nado?"Greg swims 100 yards in 52 seconds. Kelly plans to swim 150 yards at the same pace. How many seconds will it take him to complete his swim?"

Answer 1

Given in the question:

a.) Greg swims 100 yards in 52 seconds.

To be able to determine how many seconds will it take him to complete his swim, we will be applying ratio and proportion using Greg's performance at 100 yards.

We get,

`\text{ 100 yards : 52 seconds = }150\text{ yards : x}`

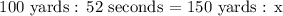
Where,

x = the time it'll take him to swim 150 yards.

Let's now compute:

`\text{ 100 yards : 52 seconds = }150\text{ yards : x }`
`\text{ }\frac{100\text{ yards}}{52\text{ seconds}}\text{ = }\frac{150\text{ yards}}{x}`
`\text{ x = }\frac{(150\text{ \lbrack{}yards\rbrack)(52 seconds)}}{100\text{ \lbrack{}yards\rbrack}}\text{ = }\frac{150(52\text{ seconds)}}{100}`
`\text{ x = }\frac{7800\text{ seconds}}{100}`
`\text{ x = 78 seconds}`

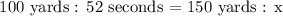
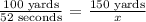
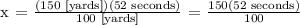
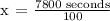
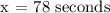
Therefore, it'll take 78 seconds for Greg to swim 150 yards.