We are given the following logistic growth function P(x)
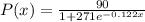
The function P(x) models the percentage of Americans who have coronary heart disease.
Here x is the age.
Let us find the percentage of 55-years old who have some coronary heart disease.
Substitute x = 55 into the function

Therefore, the percentage of 55-years old with some coronary heart disease is 67.7% (rounded to one decimal)