Given,
The measure of base of the triangle is 17.
The measure of Hypotenuse of the triangle is 19.
As, the triangle is right angled triangle.
By using Pythagoras theorem,
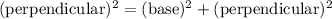
Substituting the measure of the sides of the triangle,
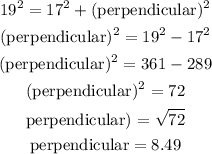
Hence, the measure of the perpendicular of the triangle is 8.49 (approx).