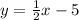Question

Write an equation in slope-intercept form for the line that passes through (4,-3) and is parallel to the line described by y=1/2+5

Answer 1

Given:

The point, (4, -3)

The line,

`y=(1)/(2)x+5`

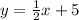
To find an equation in slope-intercept form for the line that passes through (4,-3) and is parallel to the given line:

The slope of the line is,

`m=(1)/(2)`

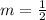
Since the given line is parallel to the new line, so the slope will be same for the both.

Using the point-slope formula,

`y-y_1=m(x-x_1)`

Substitute the point and slope we get,

`\begin{gathered} y-(-3)=(1)/(2)(x-4) \\ y+3=(1)/(2)x-2 \\ y=(1)/(2)x-2-3 \\ y=(1)/(2)x-5 \end{gathered}`

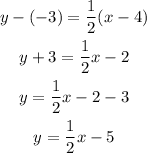
Hence, the equation in slope-intercept form for the line is,

`y=(1)/(2)x-5`