Question

Write an equation in slope intercept form of a line passing through the given point and perpendicular to the given line(0, -6);3x-2y=5

Answer 1

y = -2 /3 x - 6

Step-by-step explanation:

Here we remind ourselves that if we have an equation of the form

`y=mx+b`

then the equation of a line perpendicular to the above line is

`y=-(1)/(m)x+c`

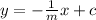
where c is the y-intercept.

Now for our case, the equation we have is

`3x-2y=5`

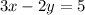
which isn't helpful since we cannot use it to find the equation of the perpendicular line.

Therefore, to make it useful, we first convert it to the slope-intercept form: y = mx + b.

Now, subtracting 3x from both sides gives

`3x-2y-3x=5-3x`
`-2y=5-3x`

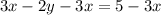
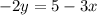
dividing both sides by -2 gives

`(-2y)/(-2)=(5-3x)/(-2)`
`y=(3)/(2)x-5`

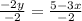
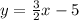
Now that our equation is in slope-intercept form, we can find the equation for the perpendicular line.

The equation of the line that is prependicular to the above line is

`y=-(1)/(3/2)x+b`
`y=-(2)/(3)x+b`

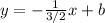
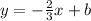
Now, we are told that this line must pass through (0, -6). Therefore, we have to find a value of b such that the above line passes through (0, -6). To find b, we put x = 0 and y = -6 into the above equation to get

`-6=-(2)/(3)(0)+b`
`-6=b\text{.}`

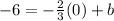
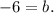
The value of b is -6.

Therefore, the equation of a line perpendicular to 3x - 2y = 5 line passing through (0, -6) is

`\boxed{y=-(2)/(3)x-6.}`