2. Exponential function:
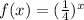
Substituting with x = 0, we get:
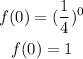
Then, f(x) passes through the point (0 ,1)
Substituting with x = -1, we get:
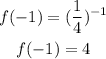
Then, f(x) passes through the point (-1 ,4)
Substituting with x = -2, we get:
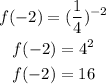
Then, f(x) passes through the point (-2 ,16)
Substituting with x = 1, we get:
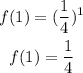
Then, f(x) passes through the point (1, 1/4)
Substituting with x = 2, we get:
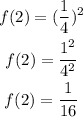
Then, f(x) passes through the point (2, 1/16)
f(x) has the form:
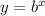
where b, the base, is between 0 and 1. This means that, when x tends to infinity, f(x) tends to zero, and when x tends to negative infinity, f(x) tends to
infinity.
Taking into account these characteristics and the points where f(x) passess, its graph is: