Step-by-step explanation:
The formula for calculating the MSE and then the confidence interval is as follows:
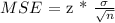
We are given that the standard deviation is $8.1 and that MSE = $0.24.
We are also told that the confidence level is 80%. The corresponding z value at 80% is 1.28
We are then required to calculate n:
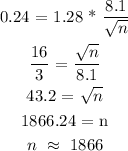
Answer: n = 1866