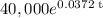continuous growth model = P e^(rt)
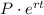
The population of a city increased from 40000 in 2000 to 50000 in 2006.
so, P = 40,000 and t = 2006 - 2000 = 6
So,
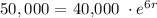
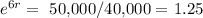
taking ln for both sides
6r = ln 1.25
r = ln1.25/6 = 0.0372
So, the continuous growth model rate for the population t years after 2000