(a)
The function
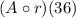
means that the input of the function is 36 and the output is the value that we get when we input 36 onto the function r which is put on the function A.
(c)
Let's find the composite function
![(A\circ r)=\pi(5.25\sqrt[]{t})^2](https://img.qammunity.org/2023/formulas/mathematics/high-school/lys607gizthpc3oton9wplyfji34yxlixm.png)
Now, we find the value of (A o r) (36):
![\begin{gathered} (A\circ r)(36)=\pi(5.25\sqrt[]{36})^2 \\ =\pi(5.25(6))^2 \\ =3117.25 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/22ibdjswxfc5axghce8ba7v6tig678db26.png)
So the size of contamination is approximately 3117.25 sq. m.
(d)
We want the time (t) when the size of the contamination would be 6250. Let's find it:
![\begin{gathered} (A\circ r)=\pi(5.25\sqrt[]{t})^2 \\ 6250=\pi(5.25\sqrt[]{t})^2 \\ (6250)/(\pi)=(5.25\sqrt[]{t})^2 \\ 5.25\sqrt[]{t}=\sqrt[]{(6250)/(\pi)} \\ \sqrt[]{t}=\frac{\sqrt[]{(6250)/(\pi)}}{5.25} \\ t=(\frac{\sqrt[]{(6250)/(\pi)}}{5.25})^2 \\ t=(\frac{\frac{\sqrt[]{6250}}{\sqrt[]{\pi}}}{5.25})^2 \\ t=\frac{(\frac{\sqrt[]{6250}}{\sqrt[]{\pi}})^2}{(5.25)^2} \\ t=((6250)/(\pi))/(27.5625) \\ t\approx72.18 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/b5m245vwvi4t12wllvvzbkgh0405mierom.png)
Answer - About 72.18 hours