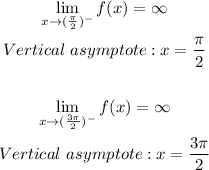Explanation
We are given the graph below of tan x:
We are required to determine limits and vertical asymptotes of the given limit.
This is achieved thus:
Limit: A limit is a value that the output of a function approaches as the input of the function approaches a given value.
Vertical Asymptote: A vertical asymptote is a vertical line that guides the graph of the function but is not part of it. It can never be crossed by the graph because it occurs at the x-value that is not in the domain of the function.
Therefore, we have:

This indicates the equation of the vertical asymptote as:

Also, we have:

This indicates the equation of the vertical asymptote as:
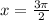
Hence, the answers review is: