There are two methods for solving for x.
Method 1:
But
Therefore,
The sketch of this is shown below:
Notice that ACB forms a triangle. And we know that the sum of angles in a triangle is 180 degrees.
The angles of the triangle are:
x, 2x and 90
Therefore, we can find x using the theorem referred to above:

Therefore, x = 30
Method 2:
The sketch of this is shown below:
Now that we have established this, we can apply the theorem that states that the sum of angles on a straight line is 180 degrees.
Thus, we can compute the value of x:
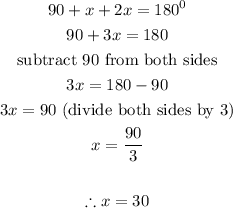
The answer is x = 30