The given problem can be exemplified in the following diagram:
Where:

To determine the value of the forces at the top and bottom we will first use the sum of moments with respect to point B. The moments in the counterclockwise direction will be considered to be positive.
The moments are:
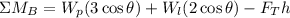
Since the ladder is not turning this means that the sum of moments is zero, therefore, we have:
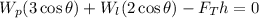
Now, since the weight is the product of the mass and the acceleration of gravity we have:
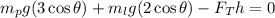
Where:
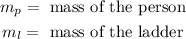
We can use the right triangle formed by the ladder and the wall to determine the cosine of the angle theta, like this:
Since the cosine is defined as:
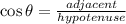
Substituting we get:
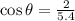
Now, we substitute the value of the cosine:
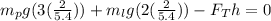
To determine the value of "h" we apply the Pythagorean theorem to the right triangle:
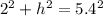
Now, we solve the squares:
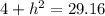
Now, we subtract 4 from both sides:
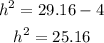
Now, we take the square root to both sides:
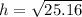
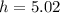
Now, we substitute the values:
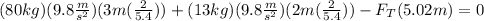
Now, we solve the operations:
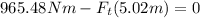
Now, we solve for the force at the top. Adding Ft(5.302m) to both sides:
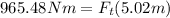
Now, we divide both sides by 5.02m:
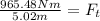
Solving the operations:
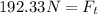
Now, to determine the forces at the bottom we will use the sum of forces. For the x-component, we add the horizontal forces, like this:
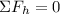
Adding the forces we get:
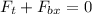
Now, we subtract the force at the bottom from both sides:

Now, we substitute:
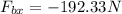
Now, we add the vertical forces:
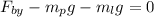
Now, we solve for the y-component:
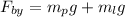
Now, we plug in the values:
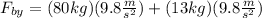
Solving the operations:
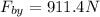
Now, the magnitude of the bottom force is given by:
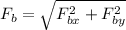
Substituting the values we get:
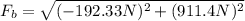
Solving the operations:
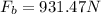
Therefore, the bottom force is 931.47N