Question

Hi there, I am a little lost on how to figure this out.

Answer 1

In this case, we'll have to carry out several steps to find the solution.

Step 01:

data:

triangles diagram

Step 02:

We must analyze the figure to find the solution.

triangle ABC:

∠ A + ∠ B + ∠ C = 180°

∠ A + 30 + 90 = 180

∠ A = 180 - 90 - 30 = 60

∠ A = 60°

BC:

`\begin{gathered} cos\text{ 30 = adjacent / hypotenuse} \\ \\ cos\text{ 30 = }\frac{BC}{16\text{ }√(3)} \end{gathered}`

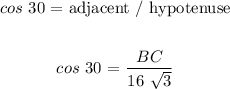
BC = 24

AC:

AC = opposite

`\begin{gathered} sin\text{ B = opposite / hypotenuse} \\ \\ sin\text{ 30 = }(AC)/(16√(3)) \\ \\ 16√(3)*sin\text{ 30 = AC} \\ \\ 13.86\text{ = AC} \end{gathered}`

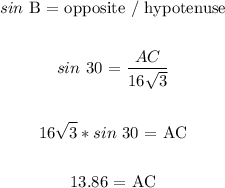
triangle ACD:

opposite = BD

adjacent = AC

BD:

`\begin{gathered} tan\text{ 30 = opposite / adjacent } \\ \\ tan\text{ 30 = }(DC)/(13.86) \\ \\ 13.86\text{ * tan 30 = DC} \\ \\ \text{8 = DC} \\ \\ BD\text{ = 24 - 8 = 16} \end{gathered}`

The answer is:

BD = 16