Question

Bonnie sits on the outer rim of a merry-go-round, and Klyde sits midway between thecenter and the rim. The merry-go-round makes one complete revolution every twoseconds. Klyde's angular velocity is:(a) Same as Bonnie's(b) Twice Bonnie's(c) Half of Bonnie's(d) One Quarter of Bonnie's(e) Four Times Bonnie's

Answer 1

Given data

The given time is t = 2 s

The merry-go-round makes one complete revolution is 360 degree

The radius of the merry-go-round is R

The angular velocity of the merry-gp-round is calculated as

`\begin{gathered} \omega=(2\pi)/(t) \\ =(2*3.14)/(2) \\ =3.14\text{ rad/s} \end{gathered}`

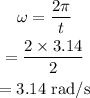
The distance of Klyde from the center is

`D=(R)/(2)`

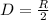
The angular velocity of any point on the merry-go-round is the same, therefore, it means that Bonnie and Klyde's have the same angular velocity