We will solve as follows:
In order to determie the lateral surface area and also the volume for the circular cylinder we operate as follows:
*Lateral surface area: We will determine the lateral surface area, this is the product of the circumference times the height:

Then:
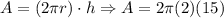
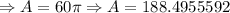
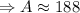
So, the lateral surface area is approximately 188 square inches.
*Volume: We have that the volume for a circular cylinder is give by:
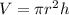
Then:
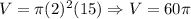
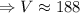
So, the volume of the cylinder is approxiately 188 cubic inches.