Question

Two angles of a quadrilateral measure 110° and 200°. The other two angles are in a ratio of2:3. What are the measures of those two angles?o ando

Answer 1

The measure of the two angles is 30° and 20°.

Explanation:

The intern angles of a quadrilateral must add up to 360 degrees. Then, if the two given angles add up to 310°, then the two missing angles must add up to:

`360\degree-310\degree=50\degree`

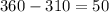
Let be x and y our missing angles, then our first equation would be:

`x+y=50`

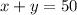
Since we also know the ratio between these angles, the second equation for the system would be:

`\begin{gathered} (x)/(y)=(2)/(3) \\ x=(2)/(3)y \end{gathered}`

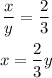
Now, plug the second equation of the system into the first one to solve the system:

`(2)/(3)y+y=50`

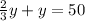
Solve for y.

`\begin{gathered} (5)/(3)y=50 \\ y=(50\cdot3)/(5) \\ y=30\text{ degrees} \end{gathered}`

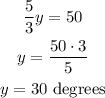
One of the angles measures 30 degrees, then the other one:

`\begin{gathered} x=50-30 \\ x=20\text{ degrees} \end{gathered}`

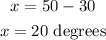
The measure of the two angles is 30° and 20°.