Question

A chemical company makes two brands of antifreeze the first brand 65% pure antifreeze the second brand is 95% pour antifreeze in order to obtain 30 gallons of mix fixture that contains 85% pure antifreeze how many gallons of each brand of antifreeze must be used

Answer 1

Given:

Let x be the amount of 65% pure antifreeze.

Let (30-x) be the amount of 95% pure antifreeze.

We need to obtain 30 gallons of mix fixture that contains 85% pure antifreeze.

To find the number of gallons in each brand:

According to the question,

Let us frame the equation,

`65\text{ \% (x)+9}5\text{ \% (30-x)}=85\text{ \% (30)}`

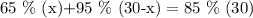
On simplification we get,

`\begin{gathered} (65)/(100)* x+(95)/(100)*(30-x)=(85)/(100)*(30) \\ (65x+95(30-x))/(100)=(85(30))/(100) \\ 65x+95(30-x)=85(30) \\ 65x+2850-95x=2550 \\ -30x=2550-2850 \\ -30x=-300 \\ x=10 \end{gathered}`

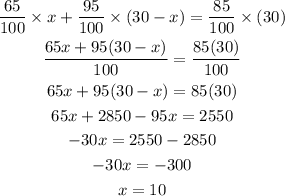
Therefore,

The amount of 65% pure antifreeze needed is 10 gallons.

The amount of 95% pure antifreeze needed is 20 gallons.