For both triangles to be similar, the corresponding sides of both triangles are always in the same ratio.
So for the corresponding sides:
1) BA ans SR, the ratio will be
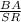
2)AC and RT, the ratio will be
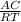
3) BC and ST, the ratio will be
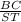
As mentioned above, the ratio between corresponding sides is always the same so that, if the triangles are simmilar the we know that:
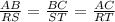
The correct option is the first one.