Question

Which of the following is true for the relation f(x)=x^2+8

Answer 1

Answer: Both the equation and its inverse are functions.

Step-by-step explanation

Given the equation:

`f\mleft(x\mright)=x^2+8`

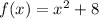
we can use the vertical line test to determine if it is a function:

As no vertical line touches the graph, then it is a function. Additionally, the inverse function can be calculating by interchanging the x and y variables in the original function:

`x=y^2+8`
`x-8=y^2`
`y=√(x-8)`

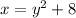
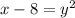
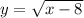
If we do the same vertical test for the inverse function we will see that both are function.