Question

How many pizza? And round ur answer to the nearest whole number and don’t intermediate calculations

Answer 1

We will have the following:

First, we determine the probability of stuffed crust and pan style:

`\begin{gathered} P_1=(161)/(894) \\ \\ P_2=(196)/(894)\Rightarrow P_2=(98)/(447) \end{gathered}`

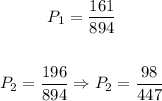
Now, we will have that the probability of P1 or P2 is given by:

`\begin{gathered} P_1orP_2=P_1+P_2\Rightarrow P_1orP_2=(161)/(894)+(98)/(447) \\ \\ \Rightarrow P_1orP_2=(119)/(298) \end{gathered}`

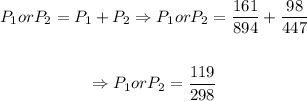
Now, from the next 1500 we will have that:

`1500((119)/(298))\approx599`

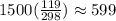
So, from the next 1500 pizzas we can expect approximately 599 pizzas to be stuffed crust or pan style.