For n = 3, x = 9, and x = 2i, we can say that one of the factors is (x - 9) as well as (x - 2i).
(x - 2i) is derived from x² = -4 which is equal to (x² + 4). Therefore, the two factors are (x - 9) and (x² + 4). To get the polynomial function, let's multiply the two factors using FOIL Method.
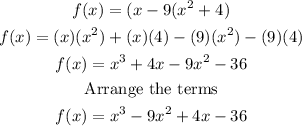
The polynomial function of the first bullet is f(x) = x³ - 9x² + 4x - 36.
For n = 3, x = -1, and x = 4 + i, we can say that the factors are:
(x + 1) , (x - (4 + i)), and (x - (4 - i))
Note: Always remember those complex zeros like x = 4 + i come in conjugate pairs.
To solve the polynomial function, let's multiply the three factors.

The polynomial function of the second bullet is f(x) = x³ - 7x² + 9x + 17.