Hello!
First, let's try to solve the following system:
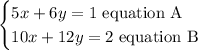
Let's solve it:
• In equation A, we will ,isolate the variable x,:
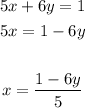
• Now, let's ,replace where's x ,in equation B ,by the value above,:
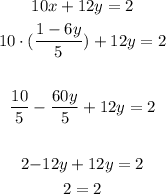
Notice that the variable y disappeared. So, we can say that this is a system with infinitely many solutions.
The solution set is:
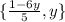
Answer B.