Total work done = work done on object + work done on cable
From the information given,
weight of object = 1500 N
weight of rope = 3N per m
height interval = 0 to 40 m
Work = force x distance
If distance = x, then, we have the integral below
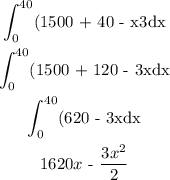
By substituting x = 40 and x = 0, it becomes
1620(40) - 3/2 * (40)^2 - 1620(0) - 3/2 * (0)^2
= 64800 - 2400
= 62400 Nm
the work done from the ground to the top of the building is 62400 Nm