
Since this can't happen, let's suppose that P=150, then:

Now we have to move the 100 to the other side of the equation with a negative sign to get this:
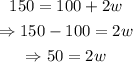
Finally, to get w, we move the 2 that's multiplying to the other side dividing the 50:
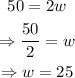
Therefore, the width of the rectangle would be 25 ft if the perimeter is 150ft, and we can see how the rectangle would look: