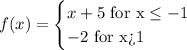1 Answer

Itsfarseen · Answer 1 · 2023-08-20T07:04:23+0000

To obtain the rule that defines the function given, we will follow the steps below:

For the first function

Step 1:

Obtain the coordinates of the line on the left-hand side of the graph

The coordinates are: (-1,4) and (-2,3)

Step 2: Get the equation of the line

=>

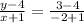
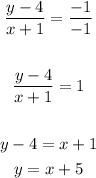
$\begin{gathered} (y-4)/(x+1)=(-1)/(-1) \\ \\ (y-4)/(x+1)=1 \\ \\ y-4=x+1 \\ y=x+5 \end{gathered}$

Hence the equation of the line given is

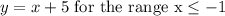
$y=x+5\text{ for the range x}\leq-1$

Step 3: Get the equation of the second line on the graph

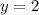
Hence, the equation of the line is

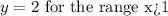
$y=2\text{ for the range x>1}$

Therefore, the rule that defines the function is:

$f(x)=\begin{cases}x+5\text{ for x}\leq-1 \\ -2\text{ for x>1}\end{cases}$

Please log in or register to add a comment.