Question

A substance has a molar mass of 175 g·mol−1 and a density of 9300 kg·m−3.i) Calculate the number of moles in 1.00 kg of the substance.ii) Calculate the volume occupied by one molecule of the substance.iii) Estimate the spacing between adjacent molecules of the substance.Assume that Avogadro’s number is 6.02 × 1023

Answer 1

The molar mass M of a sample is the ratio between its mass m and the amount of substance n that the sample contains:

`M=(m)/(n)`

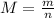
On the other hand, the density ρ of a sample is the quotient between the mass of the sample and its volume V:

`\rho=(m)/(V)`

Finally, Avogadro's Number N_A is the number of particles present in 1 mol of a substance. Then, the number of molecules N present in a sample of n mol is:

`N=n\cdot N_A`

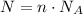
Use these relations to answer the questions.

1)

Isolate n from the first equation and replace the mass of 1.00kg and the molar mass of 175 g/mol to find the amount of substance in 1.00 kg:

2)

The volume occupied by a sample of mass m is:

`V=(m)/(\rho)`

On the other hand, the mass of one molecule can be found writing it in terms of the amount of substance and the molar mass:

`\begin{gathered} m=M\cdot n \\ \Rightarrow V=(M)/(\rho)\cdot n \end{gathered}`

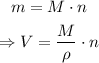
Finally, the amount of substance made up by N molecules is given by:

`n=(N)/(N_A)`

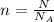
Then, the volume occupied by N molecules of a substance with molar mass M and density ρ is:

`V=(M)/(\rho)\cdot(N)/(N_A)`

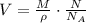
Replace M=175 g/mol, ρ=9300 kg/m^3, N=1 and N_A=6.02*10^23 to find the volume of 1 molecule:

3)

Assuming that all particles are arranged as contiguous cubes with the same volume, then the spacing between moecules is equal to the sidelength of those cubes. Since each cube has a volume of 3.126*10^-29 m^3, then the distance between adjacent molecules would be the cubic root of that amount:

`\begin{gathered} L=\sqrt[3]{V} \\ =\sqrt[3]{3.126*10^(-29)m^3} \\ =3.15*10^(-10)m \end{gathered}`

Therefore, there are 5.71 mol in 1.00 kg of the substance, the volume occupied by one molecule of the substance is 3.126*10^-29 m^3 and the spacig between adjacent molecules of the substance is approximately 3.15*10^-10 m.