ANSWER:
a. 0.2981
b. 0.0918
c. 0.9525
d. 0.4972
Explanation:
Given:
μ = 100
σ = 15
We must calculate the z-score using the following formula:

Then determine the probability with the normal table.
We calculate in each case:
a. p(X > 108)

We look for the value of the normal table:
Therefore:
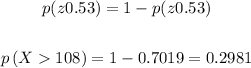
b. p(X < 80)
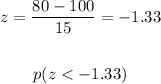
We look for the value of the normal table:
Therefore:
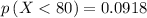
c. p (X < 125)

We look for the value of the normal table:
Therefore:
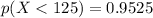
d. p (90 < X <110)
[tex]\begin{gathered} z=\frac{90-100}{15}=-0.67 \\ \\ z=\frac{110-100}{15}=0.67 \\ \\ p(-0.67We look for the value of the normal table:
Therefore:
[tex]\begin{gathered} p(-0.67