We need to find the proportion of tires that don't last more than 25,000 miles which is the same as finding the proportion that the tires last less than or equal to 25000 miles. Since this is a probability distribution finding a proportion is the same as finding a probability, hence what we need is to find the following probability:
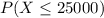
Now, since this is a normal distribution to find the probability, we will standardize the distribution given, we can do this using the z-score which is given by:

where mu is the mean and sigma is the standard deviation. Using the z-score we have:
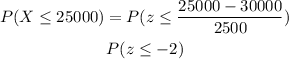
Now we just need to use a standard normal distribution table to find the probability:
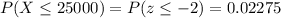
Now, that we have the probability we just multiply it by 100 to get the proportion.
Therefore, 2.28% of the tires don't last more than 25000 miles.