To obtain the relationship between x and y, the following steps are advised:
Step 1: Starting with the values in table 1, divide the values of y by the corresponding values of x, as follows:
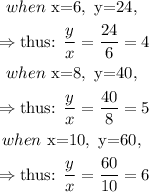
Since the value of the ratio of y to x is not constant (ranging from 4, to 5, and to 6), it means that x and y are NOT proportional.
Therefore, for Table 1, x and y are NOT proportional
Step 2: Proceeding with the values in table 2, divide the values of y by the corresponding values of x, as follows:
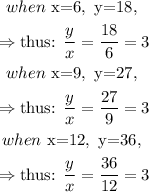
Since the value of the ratio of y to x is constant ( 3, all through), it means that x and y are proportional.
Therefore, for Table 2, x and y are proportional
Thus: y is 3 times x, for table 2