Question

(a)The length of AC is (as a decimal rounded to the nearest tenth, if needed).(b)The midpoint of AB is (as decimals rounded to the nearest tenth, if needed).

Answer 1

(a)2.2 units

(b)(-2.5, 3)

Step-by-step explanation:

From the diagram, the coordinates of A, B and C are:

A(-3,2), B(-2,4) and C(-1,3)

(a)To determine the length of AC, we use the distance formula.

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`
`(x_1,y_1)=A(-3,2$)and(x_2,y_2)=C(-1,3).$`

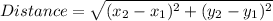
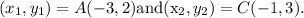
Therefore:

`\begin{gathered} AC=\sqrt[]{(-1-(-3))^2+(3-2)^2} \\ =\sqrt[]{(-1+3)^2+(1)^2} \\ =\sqrt[]{2^2+1^2} \\ =\sqrt[]{5} \\ =2.2\text{ units} \end{gathered}`

The length of AC is 2.2 units

(b)The midpoint of a line segment is calculated using the formula:

`Midpoint=\mleft((x_2+x_1)/(2),(y_2+y_1)/(2)\mright)`

Given the coordinates of A and B as follows:

A(-3,2), B(-2,4)

The midpoint of AB is:

`\begin{gathered} Midpoint=(\frac{-3_{}+(-2)}{2},\frac{2_{}+4}{2}) \\ =(-(5)/(2),(6)/(2)) \\ =(-2.5,3) \end{gathered}`

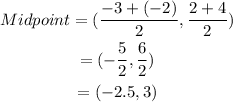
The midpoint of AB is (-2.5, 3).