Question

To calculate the cost of painting his silo, a farmer must find its height. The farmer uses a cardboard square to line up the topand bottom of the silo as shown in the diagram below. Approximate the height of the silo, rounded to the nearest foot.6 ftfeet10 ft

Answer 1

Given:

A figure with measurement is given.

Required:

Find the height of the silo.

Step-by-step explanation:

The given figure is:

Use the geometric man theorem in the right triangle ABD.

`\begin{gathered} (AC)/(BC)=(CD)/(AC) \\ AC^2=BC* CD \end{gathered}`
`\begin{gathered} CD=BD-BC \\ =BD-6 \end{gathered}`

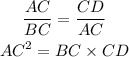
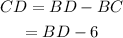
Substitute the given values.

`\begin{gathered} (10)^2=6*(BD-6) \\ 100=6(BD-6) \\ (BD-6)=(100)/(6) \\ (BD-6)=(50)/(3) \end{gathered}`
`\begin{gathered} BD=(50)/(3)+6 \\ =(50+18)/(3) \\ =(68)/(3) \\ =22.7\text{ ft} \\ \approx23\text{ ft} \end{gathered}`

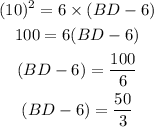
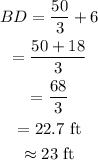
Final Answer:

The height of the silo is approximately 23 ft.