Question

Enter a rule for each function f and g, and then compare their domains, ranges, slopes, and y-intercepts.The function f(x) has a slope of -2 and has a y-intercept of 5. The graph shows the function qx).

Answer 1

so we will calculate the slope of the function g(x),

as we have two points,

(0,6) & (4,-14)

the slope will be

`\begin{gathered} m=(-14-6)/(4-0) \\ m=(-20)/(4)=-5 \end{gathered}`

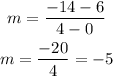
as the slope is different for f(x) and g(x),

but they both are representing the equation of the line,

so for both, the equation rule of the function will be the different

As both are continuous function then the domain and range for both the functions are the same,

The slope of f(x) = - 2

the slope of g(x) = -5

so the slope of f(x) is greater than the slope of g(x)

the equation of g(x) is,

`\begin{gathered} y-6=-5(x-0) \\ y=-5x+6 \end{gathered}`

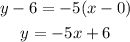
y-intercept for g(x) is 6

y-intercept for f(x) is 5 ......( Given)

so y - intercept for f(x) is less then the y intercept of g(x)

1) y = -2x + 5

2) y = -5x + 6

3) same

4) same

5) less steep

6) less