Z-score is computed as follows:
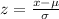
where,
x: observed value
μ: mean
σ: standard deviation
Substituting with x = 166, μ = 210, and σ = 22, we get:

Substituting with x = 254, μ = 210, and σ = 22, we get:
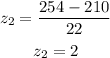
Now, we need to find P(-2From the above graph, P(-2This means that 95.44% of the sample is between the z-scores -2 and 2.
In the context of this problem, 50x95.44% = 47.72 ≈ 47 goldfish are expected to live between 166 and 254 days.