Question

I dont know how to find the area of an oval.

Answer 1

To find the area of the field, divide the shape of the field in simpler shapes.

In this case, the field can be divided in a rectangle and 2 semi circles that together form one circle. In that case, find the areas of both shapes and then find the sum of them to find the area of the field:

`\begin{gathered} A=b\cdot h \\ A=50\cdot100 \\ A=5000 \end{gathered}`
`\begin{gathered} A=\pi\cdot r^2 \\ A=\pi((50)/(2))^2 \\ A=625\pi \\ A=1963 \end{gathered}`
`A=5000+1963=6963`

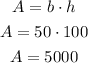
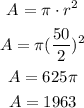
The area of the field is 6963 yd^2.