The center of the circle is (2,-3) while the radius of the circle is 2 units
Here, we want to determine the center and the radius of the given circle
Generally, we have the equation of a circle as follows;

Where (a,b) represents the center of the circle and r is the radius of the circle
We have this as follows by dividing the coefficients of x and y by 2
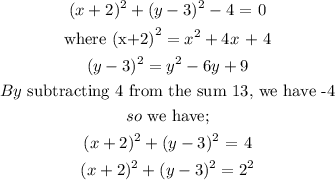
The center of the circle is (2,-3) while the radius of the circle is 2 units