Given:
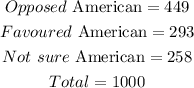
To Determine: The probability of a randomly selected American was in favor
Solution
The probability of an event A is the ratio of the number of element in A to the total number of element in the sample space
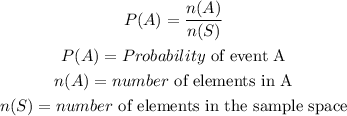
Apply the probability formula to solve for the probability of an event A is the ratio of the number of element in A to the total number of element in the sample space
Therefore,
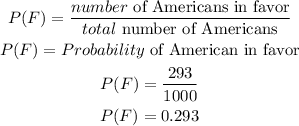
Hence, the probability of a randomly selected American was in favor is 0.293