Question

1/4, 2/4, 3/4, 4/4, describe the pattern, write the next term, and write a rule for the nth term of the sequence.

Answer 1

Arithmetic Sequence

In an arithmetic sequence, each term can be obtained as the sum of the previous term plus a fixed number, called the common difference.

To find if this is an arithmetic sequence, we subtract every consecutive term. If the result is constant, we have a common difference.

Let's subtract the second term minus the first term:

d = 2/4 - 1/4 = 1/4

Let's subtract the third term minus the second term:

d = 3/4 - 2/4 = 1/4

Let's subtract the fourth term minus the third term:

d = 4/4 - 3/4 = 1/4

Now we are sure this is an arithmetic sequence. The formula for the nth term of an arithmetic sequence is:

an = a1 + (n-1) d

Substituting:

`a_n=(1)/(4)+(n-1)\cdot(1)/(4)=(1)/(4)+(n)/(4)-(1)/(4)=(n)/(4)`

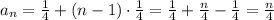
Thus, the general term is

an = n/4

To calculate the next term, we set n=5:

a5 = 5/4

Summarizing:

Rule: an = n/4

Next term: 5/4