Question

There are 99 books stacked on a shelf. The thickness of each book is either 11 inch or 22 inches. The height of the stack of 99 books is 1414 inches. Which system of equations can be used to determine xx , the number of 11-inch-thick books in the stack, and yy , the number of 22-inch-thick books?F. x+y=14x+2y=9x+y=14x+2y=9 G. x+y=92x+y=14x+y=92x+y=14 H. x+y=9x+2y=14x+y=9x+2y=14 J. x+y=142x+y=9x+y=142x+y=9

Answer 1

Given that:

the number of 1-inch thick books = x

the number of 2-inch thick books= y

Total number of stacked books = 9

The height of the stacked books = 14 inches

First equation:

Since the total number of stacked books is 9, the addition of the 1-inch thick books and 2-inch thick books must equal 9.

That is,

`x+y=9`

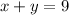
Second equation

The height of the stack of books is 14

The height of the 1-inch books =

`1\text{ }* x\text{ = }x`

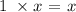
The height of the 2-inch books =

`2\text{ }* y\text{ =2}y\text{ }`

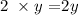
Since the total height of the stacked books is 14, the addition of the height of the 1-inch and 2-inch books must be 14.

That is,

`x+2y=14`

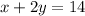
Therefore, the system of equations that can be used to determine x and y is

`\begin{gathered} x+y=9 \\ x+2y=14 \end{gathered}`

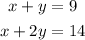
Option H is correct