First we notice that in each order, they place the same items from the menu. Let them be
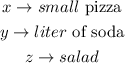
For the first order we know that they ordered 2 small pizzas, a liter of soda and a salad and that it cost 14 dollars. We can write this like

For the second order we have one small pizza, a liter of soda and three salads. That cost 15 dollars. Then
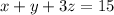
Finally, the last order was three pizzas, a liter of soda and two salads all this with a cost of 22 dollars, so
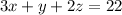
Then, from the data we have the following system of equations
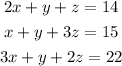
Once we solve this system we can know how much each item cost. To solve, first we are going to solve the first equation for z. Then
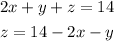
Then we plugg this value of z in the other two equations. Then

Simpligying our new equations we have
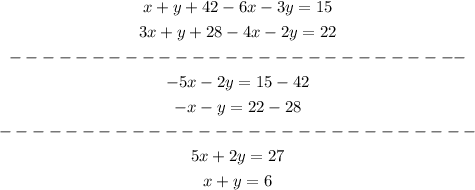
Now we have another system of equations, but in this case we only have two equations for two variables.
To solve this new system we solve the second equation for y,
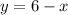
Then we plug the value of y in the first equation of our second system
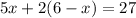
Solving for x, we have

Now that we have tha value of x, we can find the value of y from
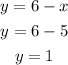
Finally, we can know the value of z from

Therefore the pizza cost 5 dollars, the liter of soda 1 dollar and the salads 3 dollars.