We will investigate the method of division of polynomials.
The notations used in the division of polynomials is as such:
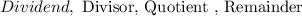
The division of polynomials in fractions is expressed as such:
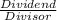
We will go ahead and express the given polynomials in a fraction form:
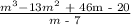
We will perform the long-division process in the following form:
We will go ahead and plug in the respective polynamials in the above displayed formulation:
The long division process is summarized in the following steps.
Step 1: Select a quoteint which can either be a ( cosntant, polynomial, or a combination ) that would eliminate the highest order of the dividend polynomial.
Note: The quotient will only be a single term!
E.g: The first quotient selected is ( m^2 ) , hence:
Step 2: Start eliminating every successive order of polynomial by subracting the result of ( quotient*divisor ) from existing polynomials.