Question

A red box initially moving at 5.1 m-s-1 collides with a blue box that is initiallystationary. After collision, the red box moves at an angle 12° above the original line ofmotion with a speed of 1.4 m-s-1, while the blue box moves with speed u at an angleof ø below the original line of motion. The two boxes have the same mass.A) Calculate the angle ø (in ° ) below the original line of motion that the blue box movesafter the collision.B) Calculate the speed v (in ms^-1) of the blue box after the collision.

Answer 1

Given data:

* The initial velocity of the red box is,

`u_1=5.1ms^(-1)`

* The initial velocity of the blue box is,

`u_2=0ms^(-1)`

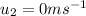
* The final velocity of the red box is,

`v_1=1.4ms^(-1)`

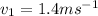
* The angle of the final velocity of the red box with the original line is,

`\theta=12^(\circ)`

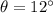
* The final velocity of the blue box is u.

* The angle of the final velocity of the blue box is denoted as

`\phi`

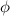
Solution:

(a). The diagrammatic representation of the given system is,

According to the law of conservation of momentum, the net momentum of the system along the x-axis before and after the collision is,

`\begin{gathered} mu_1+mu_2=mv_1\cos (\theta)+mu_{}\cos (\phi) \\ u_1+u_2=v_1\text{cos(}\theta)+u_{}\cos (\phi) \end{gathered}`

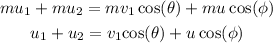
Substituting the known values,

`\begin{gathered} 5.1+0=1.4\cos (12^(\circ))+u_{}\cos (\phi) \\ 5.1=1.37+u\cos (\phi) \\ u\cos (\phi)=5.1-1.37 \\ u\cos (\phi)=3.73\ldots.(1) \end{gathered}`

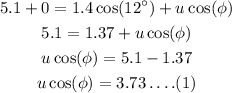
The net momentum of the system along the y-axis before and after the collision is,

`\begin{gathered} mu_1\cos (90^(\circ))+0=mv_1\sin (\theta)-mu\sin (\phi) \\ 0+0=mv_1\sin (\theta)-mu\sin (\phi) \\ v_1\sin (\theta)-u\sin (\phi)=0 \end{gathered}`

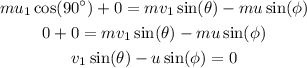
Here, the negative sign is due to the y-component of the velocity of the red box and the blue box being in opposite directions.

Substituting the known values,

`\begin{gathered} 1.4\sin (12^(\circ))-u\sin (\phi)=0 \\ 0.29-u\sin (\phi)=0 \\ u\sin (\phi)=0.29\ldots\ldots(2) \end{gathered}`

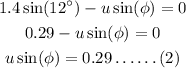
Dividing equation (2) by equation (1),

`\begin{gathered} (u\sin(\phi))/(u\cos(\phi))=(0.29)/(3.73) \\ \tan (\phi)=0.078 \\ \phi=4.446^(\circ) \end{gathered}`

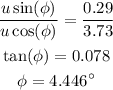
Thus, the angle of the final velocity of the blue box with the original line is 4.446 degrees.

(b). From equation (2), the final velocity of the blue box is,

`\begin{gathered} u\sin (\phi)=0.29 \\ u=(0.29)/(\sin (\phi)) \\ u=(0.29)/(\sin (4.446^(\circ))) \\ u=3.74\text{ m/s} \end{gathered}`

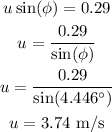
Thus, the final velocity of the blue box is 3.74 m/s.