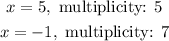Question

I am having trouble understanding where to begin with determining the zeros and their multiplicities for a factored polynomial. f(x)=(x-5)^5*(x+1)^7

Answer 1

A zero of a polynomial f(x) is a value of x such that f(x)=0.

When a polynomial is written as the product of binomial factors, we can easily find its zeroes by looking at the values of x which make each binomial equal to 0. In this case:

`f(x)=(x-5)^5(x+1)^7`

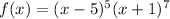
Notice that this polynomial is composed by two different binomial factors:

`\begin{gathered} x-5 \\ x+1 \end{gathered}`

If any of those factors are equal to 0, the whole polynomial will be equal to 0 since the product of 0 times any algebraic expression is always equal to 0.

Then. the zeroes of the function are the values of x such that:

`\begin{gathered} x-5=0 \\ or \\ x+1=0 \end{gathered}`

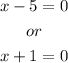
Solving each equation for x, we can see that the zeroes of the polynomial are x=5 and x=-1.

On the other hand, the multiplicity of those zeroes is equal to the exponent of the corresponding binomial. The exponent of (x-5) is 5, then the multiplicity of the x=5 zero is 5.

Similarly, the multiplicity of the x=-1 zero is 7.

Therefore, the zeroes of the polynomial f(x)=(x-5)^5*(x+1)^7 and their multiplicities are:

`\begin{gathered} x=5,\text{ multiplicity: 5} \\ x=-1,\text{ multiplicity: 7} \end{gathered}`