The equation in slope-intercept form is:

Where m is the slope and b is the y-intercept.
To find it for the given points, we can use this equation to find the slope first:

Since we have the points (2, -3) and (4, 5):
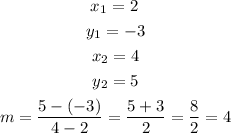
To get to the slope-intercept, we can first use the slope and one of the point to write it in the slope-point form:

And solve for y to get to the answer:
