Question

given the data below, which of the following statements correctly describes the relation of the point, (3,14) , to the line of the best fit?

Answer 1

To find the relation of the point (3,14) to the line of best fit of the data set, we need to start by finding the line of best fit of the data set.

We are going to apply the least squares method.

The line of best fit is given by the equation:

`\hat{y}=bX+a`

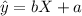
Where b is the slope of the line and a is the intercept of the line. These are the values we need to find.

1. List the x and y values given by the coordinates of the points:

Now, find the mean of the x-values and the mean of the y-values:

Find x-mean and y-mean for each value and the square of the x-mean values:

Now, find the product of (x-mean)*(y-mean):

Finally, b is given by the quotient between the sum of the products and the sum of the (x-mean)^2, so:

`b=(55.5)/(19.17)=2.90`

And a is given by:

`\begin{gathered} a=MeanY-b*MeanX \\ a=5.5-2.90*(-0.17) \\ a=5.98 \end{gathered}`

So, the line of best fit equation is:

`\hat{y}=2.90X+5.98`

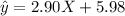
If we want to check the point (3,14), replace x=3 and find y to compare, so:

`\begin{gathered} y=2.90*3+5.98 \\ y=14.67 \end{gathered}`

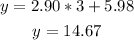
So, when x=3, the point on the line is (3,14.67)

It means the point (3,14) is quite a bit below the line.

The answer is C.