Question

A ball is thrown in the air from the top of a building. Its height, in meters above ground, as a function of time, in seconds, is given by h(t) = -4.9t^2 + 22t + 8. How longdoes it take to reach maximum height? (Round your answer to three decimal places.)

Answer 1

2.245 second

Explanation:

We have the following function:

`h\mleft(t\mright)=-4.9t^2+22t+8`

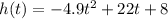
We have that the quadratic equations have the following formula:

`fx=ax^2+bx+c`

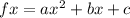
Since we have the negative leading coefficient "a", it gets the maximum at x:

`x=-(b)/(2a)`

In this case, the values would be:

a = -4.9

b = 22

Therefore, we replace and obtain the maximum value of h:

`\begin{gathered} t=-(22)/(2\cdot(-4.9)) \\ t=2.245\text{ s} \end{gathered}`

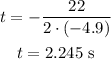
It will take 2.245 seconds to get the maximum height.