Question

Write an exponential function
`y = a {b}^(x)`whose graph passes through the given points

Answer 1

The general form of an exponential function is given as;

`y=ab^x`

Here, we are given two pointa along the curve of the graph. These are;

`(2,24)\text{ and }(3,144)`

We shall substitute the values of x and y into the general form and we'll now have;

`\begin{gathered} y=ab^x \\ \text{Where; }(x,y)=(2,24) \\ 24=ab^2 \end{gathered}`

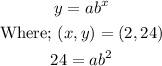
We now divide both sides by a and we'll have;

`(24)/(a)=b^2---(1)`

We do the same for the second set of coordinates and this would result in the following;

`\begin{gathered} y=ab^x \\ \text{Where; }(x,y)=(3,144) \\ 144=ab^3 \\ \text{Divide both sides by a and we'll have;} \\ (144)/(a)=b^3---(2) \end{gathered}`

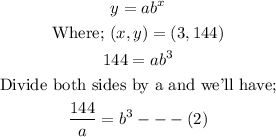
At this point, we shall refine equation (1) and make a the subject of the equation;

`\begin{gathered} (24)/(a)=b^2---(1) \\ \text{Cross multiply and we'll now have;} \\ (24)/(b^2)=a \\ a=(24)/(b^2) \end{gathered}`

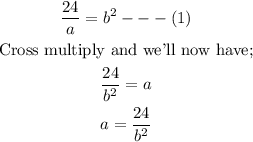
We can now substitute for the value of a into equation (2);

`\begin{gathered} (144)/(a)=b^3 \\ \text{When } \\ a=(24)/(b^2) \\ (144)/(((24)/(b^2)))=b^3 \end{gathered}`

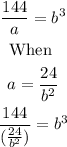
The left side of the equation can be re-arranged as follows;

`\begin{gathered} (144)/(1)/(24)/(b^2)=b^3 \\ (144)/(1)*(b^2)/(24)=b^3 \\ 6b^2=b^3 \end{gathered}`

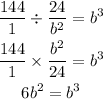
Now we divide both sides by b^2 and we have;

`\begin{gathered} (6b^2)/(b^2)=(b^3)/(b^2) \\ 6=b \end{gathered}`

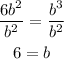
We now have the value of b as 6. we can substitute this into equation (1);

`\begin{gathered} (24)/(a)=b^2 \\ (24)/(a)=6^2 \\ (24)/(a)=36 \\ \text{Cross multiply and;} \\ (24)/(36)=a \\ (2)/(3)=a \end{gathered}`

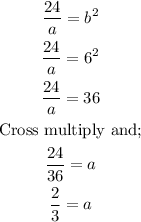
The values of a and b have now been calculated.

We can now go back and use these values to write up the exponential function using the general form;

`\begin{gathered} y=ab^x \\ \text{Where,} \\ a=(2)/(3),b=6 \\ y=(2)/(3)(6)^x \end{gathered}`

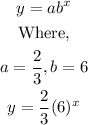
ANSWER:

`y=(2)/(3)(6)^x`