Question

A line passes through the points (-7, 2) and (1, 6).A second line passes through the points (-3, -5) and (2, 5).Will these two lines intersect? If so, what is the solution?

Answer 1

Yes, the lines intersect at (3,7). The solution is (3,7).

Step-by-step explanation:

Step 1. The first line passes through the points:

(-7,2) and (1,6)

and the second line passes through the points:

(-3,-5) and (2,5)

Required: State if the lines intersect, and if so, find the solution.

Step 2. We need to find the slope of the lines.

Let m1 be the slope of the first line and m2 be the slope of the second line.

The formula to find a slope when given two points (x1,y1) and (x2,y2) is:

`m=(y_2-y_1)/(x_2-x_1)`

Using our two points for each line, their slopes are:

`\begin{gathered} m_1=(6-2)/(1-(-7)) \\ \\ m_2=(5-(-5))/(2-(-3)) \end{gathered}`

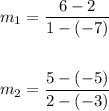
The results are:

`\begin{gathered} m_1=(6-2)/(1-(-7))=(4)/(1+7)=(4)/(8)=(1)/(2) \\ \\ \end{gathered}`
`m_2=(5+5)/(2+3)=(10)/(5)=2`

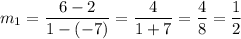
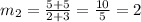
The slopes are not equal, this means that the lines are NOT parallel, and they will intersect at some point.

Step 3. To find the intersection point (the solution), we need to find the equation for the two lines.

Using the slope-point equation:

`y=m(x-x_1)+y_1`

Where m is the slope, and (x1,y1) is a point on the line.

For the first line m=1/2, and (x1,y1) is (-7,2). The equation is:

`y=(1)/(2)(x-(-7))+2`

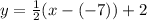
Solving the operations:

`\begin{gathered} y=(1)/(2)(x+7)+2 \\ \downarrow\downarrow \\ y=(1)/(2)x+7/2+2 \\ \downarrow\downarrow \\ y=(1)/(2)x+5.5 \end{gathered}`

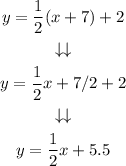
Step 4. We do the same for the second line. The slope is 2. and the point (x1,y1) is (-3, -5). The equation is:

`\begin{gathered} y=2(x-(-3))-5 \\ \downarrow\downarrow \\ y=2x+6-5 \\ \downarrow\downarrow \\ y=2x+1 \end{gathered}`

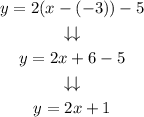
Step 5. The two equations are:

`\begin{gathered} y=(1)/(2)x+5.5 \\ y=2x+1 \end{gathered}`

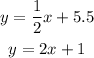
Now we need to solve for x and y.

Step 6. Equal the two equations to each other:

`(1)/(2)x+5.5=2x+1`

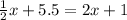
And solve for x:

`\begin{gathered} (1)/(2)x+5.5=2x+1 \\ \downarrow\downarrow \\ 5.5-1=2x-(1)/(2)x \\ \downarrow\downarrow \\ 4.5=1.5x \\ \downarrow\downarrow \\ (4.5)/(1.5)=x \\ \downarrow\downarrow \\ \boxed{3=x} \end{gathered}`

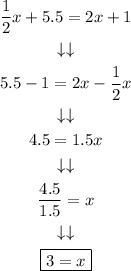
Step 7. Use the second equation:

`y=2x+1`

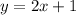
and substitute the value of x to find the value of y:

`\begin{gathered} y=2(3)+1 \\ \downarrow\downarrow \\ y=6+1 \\ \downarrow\downarrow \\ \boxed{y=7} \end{gathered}`

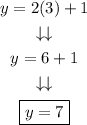
The solution is x=3 and y=7, in the form (x,y) the solution is (3,7).

Answer:

Yes, the lines intersect at (3,7). The solution is (3,7).